Estimators
\[ \renewcommand{\P}{\mathsf{P}} \newcommand{\m}{\mathsf{m}} \newcommand{\p}{\mathsf{p}} \newcommand{\q}{\mathsf{q}} \newcommand{\bb}{\mathsf{b}} \newcommand{\g}{\mathsf{g}} \newcommand{\rr}{\mathsf{r}} \newcommand{\IF}{\mathbb{IF}} \newcommand{\dd}{\mathsf{d}} \newcommand{\Pn}{$\mathsf{P}_n$} \newcommand{\E}{\mathsf{E}} \]
To recap, we have
defined a causal parameter \(\theta\) that represents the outcome \(Y\) under a general hypothetical intervention implied by the function \(\dd(a_t, h_t, \epsilon)\), and
defined the necessary assumptions to identify the expected value of \(Y\) under an intervention that replaces \(A_t\) with the output of \(\dd_t\) (applied sequentially to the natural value of treatment).
The parameter \(\theta\) is a function that could be computed if we knew the distribution of the variables (e.g., outcome regressions). Because we do not know this distribution, we need to estimate it from a sample of observed data. We now discuss how to estimate the parameter \(\theta\) from a sample.
Sequential Regression Estimator
One possible estimator is simply a plug-in estimator of the identification result. This estimator is often referred to as G-computation, or iterative conditional expectation (ICE), and it proceeds by simply estimating the regressions described in the identification result. Another way to describe this algorithm is as follows:
Initialize \(\hat \m_{\tau +1} = Y_i\).
For \(t = \tau, ..., 1\):
Using a pre-specified parametric model, regress \(\hat \m_{i,t+1}\) on \(\{A_{i, t}, H_{i,t}\}\). This gives you a predictive model \(\hat \m_t(a_t, h_t)\).
Generate predictions from this model with \(A_{i,t}\) changed to \(A^{\dd}_{i,t}\). Let \(\hat \m_t(A_{i, t}^\dd, H_{i,t})\) be these predicted values.
Repeat (iterate) the above two steps until generating predicted values \(\hat \m_1(A_{i, 1}^\dd, H_{i,1})\) at the first time point.
Take the final estimate as \(\hat{\theta} = \frac{1}{n}\sum_{i=1}^n \hat \m_1(A_{i, 1}^\dd, H_{i,1})\).
Compute standard errors using a bootstrap of steps 1 and 2; or a Delta method, if available.
A substitution estimator is nice, because its estimates are guaranteed to stay within the valid range of the outcome and it is simple to estimate. That said, its cons are major:
- In studies with multiple time points, the adjustment set can become large very quickly. For instance, consider a study with 3 covariates measured at every time point, and 10 time points. Even though we have only 3 covariates at each time point, the number of covariates in the regression of \(Y\) is 33.
- Imagine trying to correctly specify (e.g., include the appropriate interactions) a parametric model (e.g., logistic, Cox) with 33 variables.
| Pros ✅ | Cons ❌ |
|---|---|
| Simple to implement | Consistency requires correct estimation of all regressions |
| Substitution estimator | Correctness of bootstrap requires pre-specified parametric models |
Density-ratio estimation
The next three estimators all rely on estimating the density ratio
\[ r_t(a_t, h_t) = \frac{\g_t^\dd(a_t \mid h_t)}{\g_t(a_t \mid h_t)}. \]
Recall that \(\g_t^\dd(a_t \mid h_t)\) denotes the density of treatment post-intervention, i.e., the density of \(\dd(A_t, H_t)\) evaluated at \(a_t\), and that \(\g_t(a_t \mid h_t)\) denotes the density of the observed treatment under no intervention.
We will often refer to this ratio as the intervention mechanism throughout the workshop. Estimation of \(r_t(a_t, h_t)\) is fully automated in lmtp and hidden from the user. A comprehensive understanding of this process isn’t necessary to use lmtp!
We can directly estimate this density ratio with a classification trick.
Can compute the density ratio (which we can see is also the odds) in a classification problem. We use an augmented dataset with \(2n\) observations. In this new dataset, the outcome is a new variable that we make, \(\Lambda\), (defined below) and the predictors are the variables \(A_t\) and \(H_t\). In this new dataset, the data structure at time \(t\) is redefined as
\[ (H_{\lambda, i, t}, A_{\lambda, i, t}, \Lambda_{\lambda, i} : \lambda = 0, 1; i = 1, ..., n) \]
\(\Lambda_{\lambda, i} = \lambda_i\) indexes duplicate values. So if \(\Lambda_i =1\) if observation \(i\) is a duplicated value and \(\Lambda_i =0\) otherwise.
For all duplicated observations \(\lambda\in\{0,1\}\) with the same \(i\), \(H_{\lambda, i, t}\) is the same
For all the original observations, \(\lambda = 0\), \(A_{\lambda=0, i, t}\) equals the observed exposure values \(A_{i, t}\)
For all the duplicated observations, \(\lambda=1\), \(A_{\lambda=1, i, t}\) equals the exposure values under the intervention \(\dd\), \(A^{\dd}_{i,t}\)
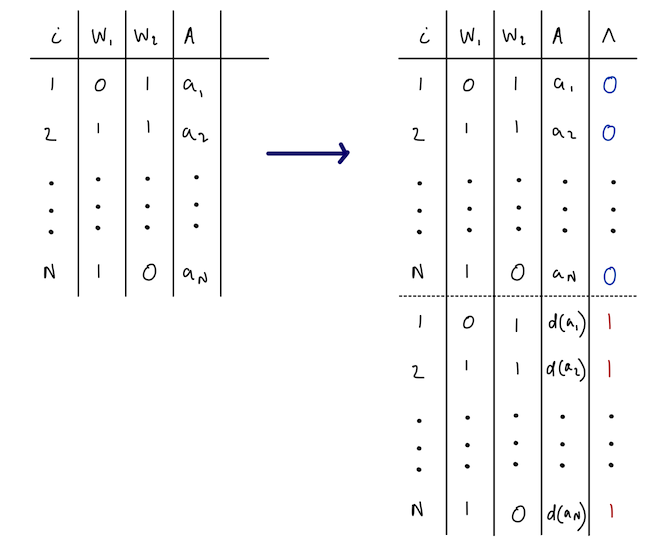
- We then estimate the conditional probability that \(\Lambda=1\) conditional on \((A, H)\) in this dataset, and divide it by the corresponding estimate of the conditional probability that \(\Lambda=0\). Specifically, denoting \(p^\lambda\) to be the distribution of the data in the augmented dataset, we have (the math behind this involves simple applications of Bayes rule):
\[ r_t(a_t, h_t) = \frac{p^\lambda(a_t, h_t \mid \Lambda = 1)}{p^\lambda(a_t, h_t \mid \Lambda = 0)}=\frac{p^\lambda(\Lambda = 1\mid A_t=a_t, H_t=h_t)}{p^\lambda(\Lambda = 0\mid A_t=a_t, H_t=h_t)} \]
Example
Consider the following example where we simulate 500 observations from this data-generating mechanism:
\[\begin{align}
L_1 &\sim \text{Normal}(0, 1) \\
A_1 &\sim \text{Bernoulli}(\text{logit}^{-1}(-1 + 1.5L_1))\\
L_2 &\sim \text{Normal}(0, 1) \\
A_2 &\sim \text{Bernoulli}(\text{logit}^{-1}(-1 + 1.5L_2 + 2A_1))\\
Y &\sim \text{Normal}(-1 - 1.2L_1 + 2.4A_1 - 2L_2 + 1.2A_2)
\end{align}\] The data has been loaded into R in the background as foo. We will use the density ratio classification trick to estimate the density ratio \(r_t(a_t, h_t)\) under the static intervention \(d(a_t, h_t) = 1\). The true value under this intervention is \(\approx 2.6\). First, we create the augmented data. We then regress the \(\Lambda\) on \(A_t\) and \(H_t\) and estimate the density ratio as the predicted odds.
Inverse Probability Weighting
We call this estimator IPW due to its similarity with the inverse-probability weighted estimator for binary treatments, but it would be more accurately referred to as simply reweighted estimator. It is based on the following alternative identification formula:
\[ \theta = \E \bigg[ \bigg\{\prod_{t=1}^\tau r_t(a_t, h_t) \bigg\} Y \bigg] \]
The algorithm is as follows:
Construct estimates of \(r_{i,t}(a_t, h_t)\) using the density ratio classification trick and a pre-specified parametric model.
Define the weights \(w_{i} = \prod_{t=1}^\tau r_{i,t}(a_t, h_t)\).
Take the final estimate as \(\hat{\theta} = \frac{1}{n}\sum_{i=1}^n \hat{w}_{i}\times y_i\).
Compute standard errors using a bootstrap of steps 1-3.
Example
Let’s apply the IPW estimator using the estimated density ratios we calculated in the previous example. We first compute the weights as the product of the density ratios.
Our estimate is then the sample average of the estimated weights times the observed outcomes.
Similarly to the sequential regression estimator, the IPW is simple to implement. However, it suffers from the same drawbacks.
| Pros ✅ | Cons ❌ |
|---|---|
| Simple to implement | Consistency requires correct estimation of all regressions |
| Uncertainty quantification requires pre-specified parametric models |
Doubly Robust Estimators
Uncertainty quantification with G-computation and IPW estimators require the estimation of nuisance parameters with correctly specified parametric models. We will now turn our attention to two non-parametric estimators that allow us to use flexible regression tools:
targeted minimum-loss based estimator (TMLE), and
a sequentially doubly-robust estimator (SDR).
Wait, what does it mean for an estimator to be doubly robust?
- For the simple case of a single time point, an estimator is considered doubly robust if it is able to produce a consistent estimate of the target parameter as long as either the outcome model is consistently estimated or the treatment (and censoring) model(s) are consistently estimated. For example:
| Time | 1 |
| Treatment | Correct |
| Outcome | Wrong |
- For time-varying setting, an estimator is doubly robust if, for some time \(s\), all outcome regressions for \(t >s\) are consistently estimated and all intervention mechanisms (treatment + censoring) for \(t \leq s\) are consistently estimated. Consider for example \(5\) time points:
| Time | 1 | 2 | 3 | 4 | 5 |
| Treatment | Correct | Correct | Wrong | Wrong | Wrong |
| Outcome | Wrong | Wrong | Correct | Correct | Correct |
- Sequential double robustness (often also referred to as \(2^\tau\)-multiply robust) implies that an estimator is consistent if for all times either the outcome or intervention mechanism (treatment + censoring) is consistently estimated. For example:
| Time | 1 | 2 | 3 | 4 | 5 |
| Treatment | Correct | Wrong | Correct | Wrong | Correct |
| Outcome | Wrong | Correct | Wrong | Correct | Wrong |
Be careful not to confuse doubly robust consistency with rate double robustness. Doubly robust consistency refers to the properties we just described. Rate double robustness refers to the property where the error of an estimator is the product of errors in estimation of two nuisance functions.
Rate double robustness is perhaps more interesting practically as it implies that the error of the estimator can be small in cases where both models are wrong!
Efficient Influence Function
Key to constructing the TMLE and SDR is the efficient influence function (EIF).
The EIF characterizes the asymptotic behavior of all regular and efficient estimators.
The EIF characterizes the first-order bias of plug-in estimators of pathwise differentiable estimands.
Before we introduce the EIF, it’s necessary to make some additional assumptions on \(A\) and \(\dd\).
The treatment \(A\) is discrete, or
If \(A\) is continuous, the function \(\dd\) is piecewise smooth invertible
The function \(\dd\) does not depend on the observed distribution \(\P\) (this means that we cannot apply these methods to odds ratio IPSI, although we can apply them to risk ratio IPSI)
These assumptions ensure that the efficient influence function of \(\theta\) for interventions \(\dd\) have a structure similar to the influence function for the effect of dynamic regimes. This allows for multiply robust estimation, which is not generally possible for interventions \(\dd\) that depend on \(\P\).
For an observation \(o\) define the function
\[ \phi_t: o \mapsto \sum_{s=t}^\tau \bigg( \prod_{k=t}^s r_k(a_k, h_k)\bigg) \big\{\m_{s+1}(a_{s+1}^\dd, h_{s+1}) - \m_s(a_s, h_s) \big\} + \m_t(a_t^\dd, h_t). \]
The efficient influence function for estimating \(\theta = \E[\m_1(A^\dd, L_1)]\) in the non-parametric model is given by \(\phi_1(O) - \theta\).
In the case of single time-point, the influence function simplifies to
\[ r(a, w)\{Y - \m(a,w)\} + \m(a^{\dd},w) - \theta. \]
Targeted Minimum-Loss Based Estimation
| Pros ✅ | Cons ❌ |
|---|---|
| Substitution estimator | not sequentially doubly-robust |
| doubly-robust | |
| can use machine learning |
The algorithm is as follows:
Construct estimates of \(r_{i,t}(a_t, h_t)\) using the density ratio classification trick and your favorite regression method.
For \(t = 1, ..., \tau\), compute the weights: \(w_{i,t} = \prod_{k=1}^t r_{i,k}(a_{i,k}, h_{i,k})\)
Set \(\tilde{\m}_{i,\tau +1}(A^\dd_{i,t+1}, H_{i,t+1}) = Y_i\).
For \(t = \tau, ..., 1\):
Regress \(\tilde{\m}_{i,t+1}(A^\dd_{i,t+1}, H_{i,t+1})\) on \(\{A_{i, t}, H_{i,t}\}\).
Using this regression, generate predictions from \(\{A_{i, t}, H_{i,t}\}\) and \(\{A^\dd_{i, t}, H_{i,t}\}\).
Denote the predictions as \(\tilde{\m}_t(A_{i,t}, H_{i,t})\) and \(\tilde{\m}_t(A^\dd_{i,t}, H_{i,t})\) respectively.
Fit the generalized linear tilting model:
\(\text{link }\tilde{\m}^\epsilon_t(A_{i,t}, H_{i,t}) = \epsilon + \text{link }\tilde{\m}_{i,t}(A_{i,t}, H_{i,t})\)
with weights \(w_{i,t}\).
\(\text{link }\tilde{\m}_{i,t}(A_{i,t}, H_{i,t})\) is an offset variable (i.e., a variable with known parameter value equal to one).
The parameter \(\epsilon\) may be estimated by running a generalized linear model of \(\tilde{\m}_{i,t+1}(A^\dd_{i,t+1}, H_{i,t+1})\) with only an intercept term, an offset term equal to \(\text{link }\tilde{\m}_{i,t}(A_{i,t}, H_{i,t})\), and weights \(w_{i,t}\).
Let \(\hat\epsilon\) be the maximum likelihood estimate, and update the estimates as:
\(\text{link }\tilde{\m}^\hat\epsilon_t(A^\dd_{i,t}, H_{i,t}) = \hat\epsilon + \text{link }\tilde{\m}_t(A^\dd_{i,t}, H_{i,t})\)
\(\text{link }\tilde{\m}^\hat\epsilon_t(A_{i,t}, H_{i,t}) = \hat\epsilon + \text{link }\tilde{\m}_t(A_{i,t}, H_{i,t})\)
Update \(\tilde{\m}_{i,t} = \tilde{\m}^\hat\epsilon_{i,t}\), \(t = t-1\), and iterate.
The final estimate is defined as \(\hat\theta = \frac{1}{n}\sum_{i=1}^n\tilde{m}_{i, 1}(A^\dd_{i, 1}, L_{i, 1})\).
Example
Let’s apply TMLE using the estimated density ratios we calculated in the previous example.
Sequentially Doubly Robust Estimator
| Pros ✅ | Cons ❌ |
|---|---|
| doubly-robust | not a substitution estimator |
| sequentially doubly-robust | |
| can use machine learning |
The SDR estimator is based on the central fact that
\[ E[\phi_t(O)\mid A_t=a_t, H_t=h_t] \approx \m_t(a_t, h_t) \]
where the approximation error is “doubly robust”. This provides a way to obtain doubly robust estimators of the regression functions \(\m_t(a_t, h_t)\)
The estimation algorithm is as follows:
Construct estimates of \(r_{i,t}(a_t, h_t)\) using the density ratio classification trick and your favorite regression method.
Initialize \(\phi_{\tau +1}(O_i) = Y_i\).
For \(t = \tau, ..., 1\):
Compute the pseudo-outcome \(\check{Y}_{i,t+1} = \phi_{t+1}(O_i)\).
Regress \(\check{Y}_{i,t+1}\) on \(\{A_{i, t}, H_{i,t}\}\). Let \(\check\m_{t}\) denote this regression.
Iterate.
The final estimate is defined as \(\hat\theta = \frac{1}{n}\sum_{i=1}^n\phi_1(O_i)\), where \(\phi_1\) is computed using \(\hat r_t\) and \(\check\m_{t}\).
Example
Let’s apply the SDR estimator. Again, we’ll use the estimated density ratios we previously estimated.
Choosing an Estimator
In general we never recommend using the IPW or sequential regression estimator. Both require the use of correctly pre-specified parametric models for valid statistical inference 🙃.
The TMLE and SDR estimators, however, are both doubly or sequentially doubly robust and can be used with machine-learning algorithms while remaining \(\sqrt{n}\)-consistent under reasonable assumptions.
| IPW | G-comp. | TMLE | SDR | |
|---|---|---|---|---|
| Uses outcome regression | ⭐ | ⭐ | ⭐ | |
| Uses the propensity score | ⭐ | ⭐ | ⭐ | |
| Valid inference with machine-learning | ⭐ | ⭐ | ||
| Substitution estimator | ⭐ | ⭐ | ||
| Doubly robust | ⭐ | ⭐ | ||
| Sequentially doubly robust | ⭐ |
While the SDR estimator may be more robust to model misspecification, the TMLE does have the advantage of being a substitution estimator. Because of this, estimates from the TMLE are guaranteed to stay within the valid range of the outcome. Taken together, this leads to the following recommendations for choosing between the TMLE and SDR:
If treatment is not time-varying, use the TMLE.
If treatment is time-varying and the parameter \(\theta\) has clear bounds, such as probabilities, beware of the SDR estimator. Use TMLE preferably.
Cross-fitting
When estimating nuisance parameters with data adaptive algorithms, you should perform a process similar to cross-validation called cross-fitting. Cross-fitting helps ensure:
that standard errors will be correct, and
can help reduce estimator bias and improve coverage of the confidence intervals.
Cross-fitting is fully automated in lmtp, but for more information we recommend reviewing Chernozhukov et al. (2018), Dı́az (2020), and Zivich and Breskin (2021).